Empedans
EMPEDANS
Genel olarak bir devre içerisinde alternatif akıma karşı gösterilen dirence empedans denir. Z sembolü ile gösterilir, birimi ohm'dur.
Direnç ve Empedans arasındaki Farklar :
- Dirençler hem AC hem DC devrelerde kullanılır, empedans ise sadece AC devrelerde mevcuttur.
- Direnç sabittir, değişmez. Empedans ise AC devrelerde ise akımın frekansına bağlı olarak değişebilir.
- Direnç faz açısına sahip değildir, empedansın büyüklüğü ve faz açısı vardır.
- Direnç bir elektromanyetik alanda tutuluğu zaman güç tüketimini ve depolanan enerjiyi temsil eder. Empedans manyetik alana maruz bırakıldığı zaman ise hem güç tüketimini hem de depolanan enerjiyi temsil eder.
Birden fazla cinsteki elemanın (direnç, bobin, kondansatör) seri, paralel veya seri- paralel bağlanması ile oluşturulan alternatif akım devresinin yerine geçebilecek aynı özellikleri verebilen tek bir eşdeğer dirence " empedans " denir.
Dirençlerde Empedans Hesabı ;
AC devrelerindeki dirençler , DC devrelerindeki gibi davranır. Temel olarak, bir direncin empedansı, yalnızca direncin direncine eşit olan gerçek kısımdan oluşur.
Anahtar kapatıldığında, direnç R'ye bir AC voltajı, V uygulanacaktır . Bu voltaj, uygulanan voltaj sinüzoidal olarak yükselip alçaldıkça sırasıyla yükselecek ve düşecek bir akımın akmasına neden olacaktır. Yük bir direnç olduğundan, akım ve gerilim hem maksimum veya tepe değerlerine ulaşacak hem de tam olarak aynı anda sıfıra düşecektir, yani eşzamanlı olarak yükselip alçalırlar.
Daha sonra bir AC direncinden geçen elektrik akımı zamanla sinüzoidal olarak değişir ve I (t) = Im x sin (ωt + θ) ifadesi ile temsil edilir; burada Im , akımın maksimum genliğidir ve θ faz açısıdır. . Buna ek olarak aynı zamanda herhangi bir akım, söyleyebiliriz i terminallerinden en ya da tepe voltaj direnci üzerinden akan R olarak Ohm kanunu ile verilecektir.
Besleme akımı ;
AC direnci tarafından tüketilen aktif güç ;
Dirençli bir bileşende faz farkı olmadığından ( θ = 0 ), ilgili fazör diyagramı şu şekilde verilir ;
2-) V (t) = 100 x cos (ωt + 30 o ) olarak tanımlanan sinüzoidal voltaj kaynağı , 50 Ohm'luk saf bir dirence bağlanır. Devreden geçen akımın empedansını ve tepe değerini belirleyin. İlgili fazör diyagramını çizin.
Direnç boyunca sinüzoidal voltaj, tamamen dirençli bir devredeki besleme ile aynı olacaktır. Bu voltajı zaman alanı ifadesinden fazör alanı ifadesine dönüştürmek bize şunu verir ;
Kapasitörlerde Empedans Hesabı ;
Kapasitörler, bir devreye belirli bir kapasitans katan bileşenlerdir. Elektrik enerjisini bir elektrik alanı şeklinde geçici olarak depolamak için kullanılırlar.
- İdeal bir kapasitörün direnci sıfırdır.
- İdeal bir kapasitörün reaktansı ve dolayısıyla empedansı, tüm frekans ve kapasitans değerleri için negatiftir.
- Bir kapasitörün etkin empedansı (mutlak değer) frekansa bağlıdır ve ideal kapasitörler için her zaman frekansla azalır.
İndüktörlerde Empedans Hesabı ;
İndüktörler, bir devreye belirli bir endüktans katan bileşenlerdir. Elektrik enerjisini manyetik alan şeklinde geçici olarak depolamak için kullanılırlar. Bu nedenle, zaman alanında gerilime kıyasla akımı 90 derece geciktirmek için indüktörler kullanılır.
- İdeal bir indüktörün direnci sıfırdır.
- İdeal bir indüktörün reaktansı ve dolayısıyla empedansı, tüm frekans ve indüktans değerleri için pozitiftir.
- Bir indüktörün etkin empedansı (mutlak değer) frekansa bağlıdır ve ideal indüktörler için her zaman frekansla artar.
Kısaca gösterecek olursak ;








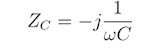




Yorumlar
Yorum Gönder